<<Previous

Intro

ch1

ch2

ch3

ch4

ch5

ch6

ch7

ch8

ch9

ch10

Next>>

ch11

ch12

ch13

ch14

ch15

ch16

ch17

ch18

ch19

ch20

ch21

The Observed Properties of Liquid Helium
at the Saturated Vapor Pressure

Russell J. Donnelly and Carlo F. Barenghi

The equilibrium and transport properties of liquid 4He are deduced from experimental observations at the saturated vapor pressure. In each case the bibliography lists all measurements known to us. Most of these quantities are represented by cubic spline fits of a data base adopted from the cited literature by subjective judgement. Quantities reported here include density, thermal expansion coefficient and dielectric constant, superfluid and normal fluid densities, first, second, third and fourth sound velocities, specific heat, enthalpy, entropy, surface tension, ion mobilities, mutual friction ,viscosity and kinematic viscosity, dispersion curve, structure factor, thermal conductivity, latent heat, saturated vapor pressure, thermal diffusivity and Prandtl number of helium I, displacement length and vortex core parameter in helium II. This report differs from an earlier one by J. S . Brooks and R. J. Donnelly (J. Phys. Chem. Ref. Data 6, 51, 1977) in which equilibrium properties of helium II were calculated from neutron scattering experiments over a range of temperatures and pressures.

Key words:, helium I, helium II, observed equilibrium and transport properties of liquid 4He.


Table of Contents

Chapter	Title	Page
	Introduction Acknowledgements List of Tables List of Figures	ii v vi ix
1	Density, thermal expansion and dielectric constant	1
2	Superfluid and normal fluid densities	11
3	First sound velocity	20
4	Second sound velocity	30
5	Third sound velocity	40
6	Fourth sound velocity	43
7	Specific heat and enthalpy	49
8	Entropy	66
9	Surface tension	75
10	Ion mobilities	83
11	Mutual friction	100
12	Viscosity and kinematic viscosity	105
13	Dispersion curve	114
14	Structure factor	120
15	Thermal conductivity	128
16	Latent heat	137
17	Saturated vapor pressure	145
18	Thermal diffusivity of helium I	151
19	Prandtl number of helium I	153
20	Displacement length and vortex core parameter	154
Appendix	Programs for spline evaluation	156

List of Figures

1.1	The recommended values of the density of liquid 4He as a function of temperature at the saturated vapor pressure................................................	1223
1.2	The recommended values of the thermal expansion coefficient of liquid 4He at the saturated vapor pressure as a function of temperature..............................	1223
1.3	Detail of the recommended values for the thermal expansion coefficient of liquid 4He near the lambda transition.....................................................	1223
1.4	The recommended values of the thermal expansion coefficient of liquid 4He at low temperatures......................................................................................	1223
2.1	Recommended values of the superfluid density of helium II as a function of temperature......................................................................................................	1226
2.2	Recommended values of the superfluid density of helium II near the lambda transition......................................................................................................	1226
2.3	The fractional deviation of the adopted database from the recommended values for the superfluid density of helium II expressed in percent.......................................	1226
3.1	The recommended values for the first sound velocity of liquid 4He as a function of temperature at saturated vapor pressure............................................................	1228
3.2	Detail of the recommended values for the first sound velocity of liquid 4He about the lambda transition........................................................................................	1228
3.3	The fractional deviation of the adopted database from the recommended values of the velocity of first sound in liquid 4He expressed in percent.................................	1228
3.4	The fractional deviation of the adopted database from the recommended values of the velocity of first sound in liquid 4He expressed in percent.for ............................	1228
3.5	The fractional deviation of the adopted database from the recommended values of the velocity of first sound in liquid 4He expressed in percent. for ..........................	1230
4.1	The recommended values for the velocity of second sound in helium II as a function of temperature at saturated vapor pressure.........................................................	1231
4.2	Detail of the recommended values for the second sound velocity in helium II about the lambda transition.........................................................................................	1231
4.3	The fractional deviation of values of the adopted data base from the recommended values for the velocity of second sound in helium II expressed in percent................	1231
6.1	The recommended values for the velocity of fourth sound as a function of temperature at the saturated vapor pressure.......................................................	1235
6.2	The fractional deviation of values of the adopted database from the recommended values for the velocity of fourth sound in helium II expressed in percent.................	1235
7.1	The recommended values for the heat capacity of liquid 4He as a function of temperature at saturated vapor pressure............................................................	1236
7.2	The recommended values for the heat capacity of liquid 4He at saturated vapor pressure near expressed as Cs vs log10 | T-T|...................................................	1236
7.3	The fractional deviation of values of the adopted database from the recommended values for the heat capacity of liquid 4He expressed in percent	1237
7.4	The fractional deviation of values of the adopted database from the recommended values for the heat capacity of liquid 4He near the lambda transition for T < T......	1237
7.5	The fractional deviation of values of the adopted database from the recommended values for the heat capacity of liquid 4He near the lambda transition for T > T......	1237
7.6	Values for the enthalpy of liquid 4Hehelium at saturated vapor pressure, obtained by integration of the recommended values of the heat capacity............................	1237
7.7	Fractional deviation of the spline fit of the recommended values of the enthalpy from the enthalpy integrated from recommended values of the heat capacity.........	1237
8.1	The recommended values of the fountain pressure entropy of liquid 4He as a function of temperature at saturated vapor pressure..........................................	1243
8.2	The fractional deviation of values of the adopted database from the recommended values for the fountain pressure entropy of liquid 4He expressed in percent..........	1243
8.3	The recommended values of the entropy of liquid 4He obtained by integration of the heat capacity spline.......................................................................................	1243
8.4	The fractional deviation of values of the adopted database from the recommended values for the entropy integrated from the heat capacity spline..............................	1244
9.1	The recommended values of the surface tension of liquid 4He as a function of temperature at saturated vapor pressure............................................................	1245
9.2	Detail of the surface tension about the lambda transition	1246
9.3	The fractional deviation of the values of the adopted database from the recommended values of the surface tension of liquid 4He expressed in percent	1246
10.1	Positive ion mobility as a function of temperature along the saturated vapor pressure line...................................................................................................	1248
10.2	Deviation of the database from the spline fit to log10 +......................................	1248
10.3	The recommended values of the negative ion mobility as a function of temperature at saturated vapor pressure..............................................................................	1248
10.4	The fractional deviation of values of the adopted database from the recommended values for the log10 - in liquid 4He expressed in percent....................................	1248
12.1	The recommended values of the viscosity of liquid 4He as a function of temperature at saturated vapor pressure..............................................................................	1255
12.2	The fractional deviation of values of the adopted database from the recommended values for the viscosity of liquid 4He expressed in percent.....................................	1255
12.3	The recommended values of the kinematic viscosity of liquid 4He v=/p, as a function of temperature at the saturated vapor pressure........................................	1256
13.1	Energy E in degrees Kelvin of elementary excitations in helium II as a function of wave number Q (Ref.12)....................................................................................	1258
13.2	Group velocity of elementary excitations in helium II as a function of wave number Q (Ref.12........................................................................................................	1259
13.3	The fractional deviation of values of the adopted database from the recommended values for the dispersion curve for liquid 4He, expressed in percent.......................	1259
14.1	The recommended values for the structure factor of liquid 4He as a function of wave number............................................................................................................	1260
14.2	The fractional deviation of values of the adopted database from the recommended values for the structure factor expressed in percent.............................................	1262
15.1	The recommended values for the thermal conductivity of liquid 4He as a function of temperature at the saturated vapor pressure......................................................	1262
15.2	Log plot of k vs | T - T|...................................................................................	1262
15.3	Deviation of the database from the spline fit of thermal conductivity expressed in percent............................................................................................................	1265
16.1	The recommended values for the latent heat of vaporization of liquid 4He as a function of temperature at the saturated vapor pressure........................................	1265
16.2	Detail of the recommended values latent heat of vaporization about the lambda transition............................................................................................................	1265
16.3	The fractional deviation of values of the adopted database from the recommended values for the latent heat expressed in percent......................................................	1265
17.1	The recommended values for the saturated vapor pressure (in Pa) of liquid 4He calculated from the spline...................................................................................	1267
17.2	Log10 of the saturated vapor pressure curve (in Pa) of liquid 4He.............................	1267
17.3	The fractional deviation of values of the saturated vapor pressure of 4He calculated with the spline from those calculated with the ITS-90 equations expressed as percent..............................................................................................................	1267
17.4	Deviations in temperature ?T corresponding to the deviations in pressure shown in Figure 17.3........................................................................................................	1267

Introduction

Liquid helium has been studied intensively for more than three quarters of a century: indeed one may advance the claim that it is the most studied pure substance in the history of science. Our group, pursuing certain theoretical topics in the 1960's, became aware of the unwelcome impact of faulty data in testing ideas on the theory of superfluidity. We therefore began a collection of well-documented data which first appeared in the book by Donnelly1 and a further set of useful tables appeared in the book by Wilks2. As research progressed, it became evident that the pressure of liquid helium is just as significant a parameter as temperature, and it was recognized that it would be decades before enough data would exist to make a critical compilation of the properties of liquid helium as a function of pressure and temperature.

A ray of hope emerged when inelastic neutron scattering studies began to appear, and one gradually learned the true experimental nature of the dispersion curve for elementary excitations in He II. Early work by Bendt, Cowan and Yarnell3 showed that the thermodynamic properties of He II along the vapor pressure line could be extracted from neutron scattering measurements with reasonable success. Unfortunately, it soon appeared that the parameters of the spectrum are both temperature-dependent and pressure-dependent. The temperature dependence was especially troublesome because the standard formulas of statistical mechanics, and indeed quantum mechanics, have no direct provision for handling temperature-dependent energy levels. This problem was studied by Donnelly and Roberts4 who produced an approximate method for the computation of thermodynamic quantities which can be used when the energy levels are known from experiment. The methods of Donnelly and Roberts then were used by Brooks and Donnelly5 to produce their report "The Calculated Thermodynamic Properties of Superfluid Helium-4" which evolved through a thesis, a preliminary edition, and finally a publication over the period 1972-77. Brooks and Donnelly's tables of equilibrium properties have the advantage that they are thermodynamically self-consistent over the entire temperature-pressure (T,P)-plane; that is, they obey Maxwell's relations; they have the disadvantage that they are not useful near the -transition. Further, they are based on some ad-hoc assumptions such as the concept of an "effective sharp spectrum" whose validity is not known except by the test of utility. Nevertheless, those calculated tables still stand as the most reliable general guide to the equilibrium properties of He II over the whole (T,P)-plane as shown in the diagram below.

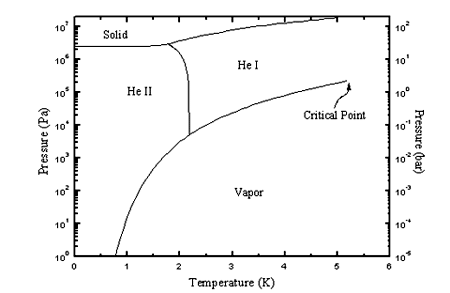
With the issue of this study, we are presenting a comprehensive collection of the experimental data for the equilibrium and transport properties of pure liquid 4He.

The format used will generally be the following:

. Chronological bibliography of all known measurements (placed at the end of each chapter)

2. Selection of an “adopted database” obtained by subjective judgment. Note that the temperature ranges given in the adopted table base are in the temperature scale used by the authors, not necessarily T90.

3. To facilitate the description of the adopted database we have chosen a table format. The key # is used to give the origin of the data in the adopted database and leads to the literature citation. To save space we have used E+2, E+1, E+0, E-1 instead of 102, 10, 1, 10-1 etc.

4. Table of the adopted database. Temperature values in the adopted database are in T90 Note that the ITS-90 is not defined below 0.65 K. Values below 0.65 K are on the thermodynamic scale.

5. Table of recommended values obtained by the cubic spline fits of the data.

6. Curves showing the recommended values and the fractional deviation of values of the adopted database from the recommended values.

If f(T) is the quantity being discussed we define the fractional deviation in percent as

=(f _measured -f _calculated)/f _measured X 100

7. Tables of recommended values.
In most cases we have represented the data by cubic splines. A routine to evaluate these splines is included as an Appendix.

A word is required about significant figures in this study. Most (but certainly not all) of the data here is of order one percent in accuracy so that three figures should be adequate to represent it. Furthermore, the spline fit returns all the figures yielded by the calculation. Nevertheless we have usually given recommended data to four figures simply as a compromise among data of varying precision and accuracy.

A second problem is that some data such as specific heat spans an enormous range: over 5 decades in (see the recommended values in Chapter 7).

Temperature resolution is another problem. Modern thermometry resolves temperatures throughout the region to 4K with millikelvin to microkelvin precision. However the absolute temperature is not known to anything like this resolution. Most superfluidity researchers have used the T58 vapor pressure scale and their data is keyed to it for better or for worse. However the T90 scale is now used to calibrate thermometers, and we have undertaken the somewhat risky task of converting our T58 tables, which were circulated as a Report of the Department of Physics, to T90. The method of doing this was outlined in an MS thesis by Ling Lui in 1992 6.

In some cases we have recalculated temperatures ourselves after discussion with the authors. Thus a few figures appear which are not exactly those originally published. Naturally, the biggest changes in data, and greatest sensitivity to the T90 occurs near the lambda transition.

An even more bizarre situation appears in representing data near the lambda transition. Here the difference in temperature from the lambda transition is what is really measured, and these days, that can be done in some cases to nanokelvin resolution, especially above 2.17K. Thus in the last 100 millikelvin below and above the lambda point we have had to carry many significant figures because our spline fits the temperature. It is the joy of least squares cubic splines that they can represent data near a singular point like the lambda point. The down side is that we are printing data on temperature with many figures which were really measured as deviations. The reader will appreciate that any strict treatment of printing only significant figures will lead to a typographic nightmare.

We can summarize the situation by stating that we are usually erring on the side of carrying too many figures, and that the antidote is a quick glance at the normalized deviation curve.

In making the spline fits, we have tried to get as good a fit to the data as possible, especially near the lambda point. But these fits should under no circumstances be relied upon for scaling investigations.

Note that we have listed a number of quantities in the units normally used by the low temperature physics community. Conversion to SI units has been made in several cases in this report and conversion factors to SI are given wherever needed.

Our initial work was done using HP BASIC. We list spline evaluation programs in the Appendix in HP BASIC. In addition, FORTRAN, C, and HP48SX subroutines are given.

References

1. Donnelly, R. J.; P.E. Parks and W.I. Glaberson. "Experimental Superfluidity." University of Chicago Press, Chicago (1967)

2. Wilks, J. "Liquid and Solid Helium." Clarendon Press, Oxford (1967)

3. Bendt,P.J., R.D. Cowan, J.L. Yarnell. "Excitations in Liquid Helium: Thermodynamic Calculations." Phys. Rev. 113, 1386-1395 (1959)
4. Donnelly, R.J. and P.H. Roberts. J. Low Temp. Phys. 27, 687-736 (1977)

5. Brooks, J.S. and R.J. Donnelly, J. Phys. Chem. Ref. Data 6, 51-104 (1977)

6. Lui, Ling, “The Observed Properties of Liquid Helium on the ITS-90.” MS Thesis, University of Oregon (unpublished).

Acknowledgements

These tables in their present form have been in preparation for some 30 years. Many students and visitors have had a part in preparing them. From my own group there have been (in addition to my co-author) James Brooks, whose thesis made all this possible, Thomas Wagner, James Donnelly, Christa Laursen, Ling Lui, James Mulder, Robert Riegelmann and most recently, Steve Stalp, Steve Hall and Rose Lowe-Webb.

Professor Paul Roberts contributed by working out the theory of extracting thermodynamic properties when energy levels determined by neutron scattering are temperature dependent, and Dr. R. N. Hills introduced us to the advantages of cubic splines and wrote the first programs to generate and evaluate splines, which we still use today. Ron also helped develop the present tables format.

Ling Lui began the enormous task of converting these tables to T90 as her master’s thesis. This thesis explains the technical details of her method of converting to T90.In doing so we had to consult a number of experts on temperature scale. These were Marty Durieux, Ralph Hudson, Michael Moldover, Richard Rusby and Clayton Swenson.

When preliminary issues of these tables have been circulated, we have received many suggestions and new measurements. These have come from Guenter Ahlers, Dennis Greywall, Horst Meyer, Jay Maynard and Isadore Rudnick.

This research was supported by the National Institute of Standards and Technology, Office of Standard Reference Data, under grant number NBS788, by the National Science Foundation through the years under a number of grants entitled “The Physics of Fluids” and currently, by the National Science Foundation under grant DMR-9529609.